Resultados de la metrica para el filtrado de la cancion.

Saludos a todos:

Se que muchos aunque no lograron el primer lugar, hicieron un gran trabajo. Me gusto mucho sentir que han trabajado y que estan en capacidad de disenar filtros digitales. El reto es mudar los filtros a otros ambientes computacionales como los FPGA, los DSP, y en general a sistemas de computacion embebidos o empotrados. Si ustedes estan interesados sigamos en contacto para seguir creciendo.

En el fin de semana hare un post con la forma de hacer la metrica y la implementacion que yo use con los resultados que obtuve. Esten pendientes.

Ahora si van los resultados:

ID      Valor de metrica 
176878    6.78060E+00
177979    6.78060E+00
117797    1.42680E+03
95429    1.42680E+03
175896    2.69400E+03
126146    2.69400E+03
167933    6.29240E+03
190832    6.29240E+03
129656    7.18200E+03
116597    7.18200E+03
175774    1.38230E+04
117922    1.38230E+04
176567    3.09240E+04
175565    5.06700E+04
179280    5.06700E+04
167085    7.70010E+04
169414    7.70010E+04
178937    8.08680E+04
176363    8.08680E+04
178227    8.44830E+04
176690    8.44830E+04
178419    INF
179093    INF


Los dos ganadores los espero en el laboratorio D304 a las 4:30 PM para la sustentacion de su trabajo.

Como bajar un archivo de una pagina web....

Saludos:

He visto que han tenido problemas bajando el archivo de audio de la pagina del curso. Bueno por eso mismo he creado un tutorial para bajar el archivo de audio.

Paso 1: Accede a la pagina: caceros.docentes.upbbga.edu.co
Paso 2: Busca el area donde dice Aerosmith.wav. Y se da click derecho, debera ver algo como esto:

Seleccionar "Guardar destino como..." o "Save link as...". Con esto arranca una ventana para descargar que terminara con lo siguiente:

Espero les sirva este post.

Diseno de un filtro pasabanda....

Saludos en esta oportunidad voy a mostrar como disenar un filtro pasabanda.

Asumimos que tenemos una senal de entrada que tiene 3 componentes senosoidales puras de 2KHz, 3KHz y 4KHz.

PROBLEMA
Deseamos eliminar las componentes senosoidales de 2KHz y 4KHz con una atenuacion de al menos 40 dB y dejar pasar la senal de 3KHz con una atenuacion de 0 dB y rizado de 3 dB en la banda de paso.

El problema nos obliga a pensar que requerimos de un filtro que deje pasar solamente la senal de 3KHz y bloquee las demas. Este filtro existe y se llama pasabanda porque deja pasar frecuencias entre un rango especificado como banda de paso. y lo que este por encima y por debajo de este rango es rechazado (banda de rachazo). Mirar la figura para entender como funciona:

 El resultado de correr este programa: demofiltro.m. Una forma grafica de ver como actua el programa sobre las senales.

Las salidas del programa demofiltro.m estan a continuacion:

Espectro de la senal de entrada x:

Los picos son de izq a derecha: 2KHz, 3KHz y 4 KHz. Los picos que aparecen en 6KHz, 7KHz y 8KHz el resultado de la reflexion de la DFT en la frequencia de muestreo que es 10KHz.

El filtro que se diseno tiene las siguientes especificaciones:

Respuesta en frecuencia del filtro, noten que la Magnitud esta en dB, lo que hace que la grafica se vea distinto a lo que uno esta acostumbrado. 40 dB es una atenuacion barbara....como ejercicio traten de sacar cuando es 40 dB en relacion.

Comprabacion de banda de paso. Las frecuencias de paso son 2750Hz y 3250Hz

Comprobacion de banda de rechazo.

La salida del filtro es:

Aparece la componente de 3KHz y las componentes de 2KHz y 4KHz estan tan atenuadas que es como si hubieran desaparecido.

Espero que les sirva este post.

Reconstruccion de un senal pulso periodica

De acuerdo al numero de coeficientes de la serie de Fourier que uno adicione se obtendra una aproximacion mayor a la senal original. En este caso estamos hablando de la siguiente senal x(t):

Los coeficientes de la serie de Fourier para esta senal es:

La senal se reconstruye usando la siguiente formula:

 
Y estos son las senales para diferentes valores de N:
El programa esta aca.
N=2:

 

N=5

 N=10

N=30

Coeficientes de Fourier de una senal senosoidal.

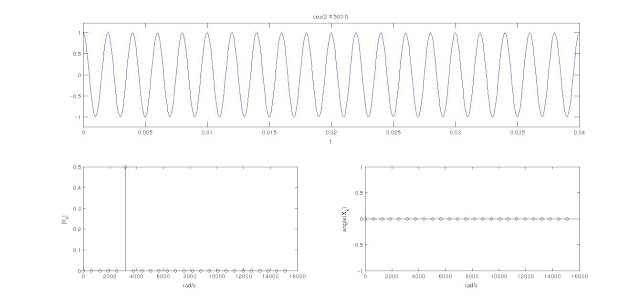
Los coeficientes de una senal periodica senosoidal de una frecuencia fija, puede ser computados usando la toolbox simbolica de Matlab. Lo interesante de esta senal es que los coeficientes tiene un solo componente en la frequencia de la senal que es distinto de cero, los demas componentes son cero.

A continuacion se muestran varios resultados para la ejecucion del programa fourierseries.m tomado del libro del curso. El codigo del programa puede conseguirse aca. No olviden que hay que tener paciencia al ejecutar el codigo...a veces se demora muchisimo.

[X w]=fourierseries('cos(2*pi*500*t)',1/100,25);

Ahora si agregamos una fase:

[X w]=fourierseries('cos(2*pi*500*t+pi/2)',1/100,25);

se obtiene:

Y ahora vamos a duplicar la frecuencia:

[X w]=fourierseries('cos(2*pi*1000*t)',1/100,25);

se obtiene:

cos(2*pi*t+ pi/4) es par o impar?

Alguien me hacia la pregunta que titula este post....la verdad es que si usamos Matlab para graficas la funcion con el siguiente codigo tendremos:

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% PROGRAMA QUE GRAFICA LA FUNCION
% cos(2*pi*t + pi/4)
% Programado por: Cesar A Aceros
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

t=sym('t');
y=cos(2*pi*t + pi/4);

ezplot(y,[-1,1]);
grid on

Se obtiene la siguiente grafica:

Si la funcion es par cos(x)=cos(-x). Si hacemos t=0.6 y t=-0.6. Se obtienen los puntos que estan en la grafica. Y los valores de la funcion dan distintos por lo cual podemos demostrar que la funcion no es par, ni impar.

>> cos(2*pi*.6+pi/4)

ans =

   -0.1564

>> cos(2*pi*-.6+pi/4)

ans =

   -0.9877

El caso que habiamos considerado de t=-1 y t=1 para tiempo es un caso especial que aunque dan el mismo valor, son solo un punto y no se genera una simetria que indique que es impar o par. Esto se puede ver en la evaluacion para t=-1 y t=1 en el command line de Matlab.

>> cos(2*pi*-1+pi/4)

ans =

    0.7071

>> cos(2*pi*1+pi/4)

ans =

    0.7071

Comprobacion de 3 tipos de senales periodicas/no periodicas.

El proposito de este post es demostrar 3 tipos de senales y su comportamiento periodico/ no periodico.

Primeramente vamos a considerar la suma de una senal con una constante y veremos su salida.

En el codigo presentado a continuacion se suma una senal senosoidal de w=2*pi con una constante 5.

 %%%%%%%%%%%%%%%%%%%
% Autor: Cesar Aceros
% Fecha: Feb 15, 2012
% Suma de una senosoidal con una constante
%%%%%%%%%%%%%%%%%%%
t = sym('t');
x = cos(2 * pi * t);
y = 5;
z = y + x;
h = ezplot(z,[0,4])
grid

La salida a este codigo es: